Dear James,
There weren’t calculators or computers in medieval Europe. But there were math duels.
Mathematicians would gather in public squares and pose tricky math problems to each other. Then they raced to solve them. Victors might win money, fame or a university job. (Sadly, this isn’t how I got my job.)
People still noodle on difficult math puzzles for work and fun today.
That’s what my friend Daryl DeFord told me. He’s a mathematician at Washington State University.
“That’s really what math is all about,” he said. “You find something that doesn’t quite make sense, and you keep poking at it until it does.”
Some math problems are difficult because they take a long time to solve. Others are tricky because no one has ever solved them.
There are even modern math contests—a lot like those medieval math duels. In 2000, the Clay Mathematics Institute named seven Millennium Prize Problems. Each of these math problems has a $1 million prize for the solver.
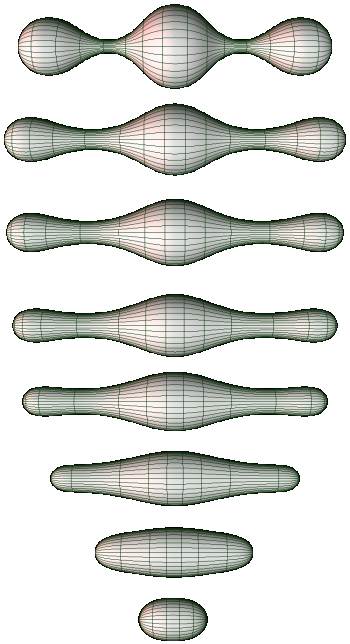
So far, just one Millennium Prize Problem has been solved. In 2003, Grigori Perelman proved the Poincaré Conjecture. That’s about how shapes can be stretched or bent in different dimensions. To figure it out, Perelman used Ricci flow—shown in this image. That smooths out a shape in space. It’s like imagining the shape is rubber and heating it to even out any bumps or lumps. But Perelman turned down the prize money. He was only interested in the work.
The Riemann Hypothesis is one of the most famous problems in that set. It’s about prime numbers. That’s any whole number that can only be divided by 1 and itself—like 2, 3, 5, 7 and 11.
Back in 1859, a mathematician said there’s probably a pattern to describe how prime numbers are distributed. But so far nobody can prove that pattern exists—even though they’ve been working on it for more than 165 years.
Those kinds of math problems require advanced math knowledge. But there are technically simpler math mysteries, too.
The odd perfect number problem might be the oldest math problem of all. A perfect number is one whose proper divisors add together to equal the number itself. The number 6 is a perfect number because its divisors—1, 2 and 3—add up to 6.
But nobody has ever found an odd perfect number. People have been looking for one for thousands of years.
DeFord told me many mathematicians have personal math puzzles, too. These are math problems that grab their attention. They work on those problems for years or even decades.
DeFord has a problem like that.
Let’s say you have a 4 x 4 grid—so a page with 16 squares. And you have four shapes made of four blocks stuck together. How many ways can you cover the grid with those pieces? The answer is 117.
We know the answers for grids up to 9 x 9 with shapes made of nine blocks. (The 9 x 9 answer is 706,152,947,468,301.)
“The number of solutions for the 9 x 9 grid is staggeringly huge,” DeFord laughs. “Actually, one of my friends sent me a message this weekend claiming that by devoting 3TB of RAM on a super computer at Yale he will know the 10 x 10 value in the next couple of weeks—and maybe as soon as tomorrow.”
Whether that happens or not, he’s not giving up—and neither should you. I hope you take up your own im-paw-ssible math problem and make it your own.
Consider this your purr-sonal invitation to a math duel.
Sincerely,
Dr. Universe